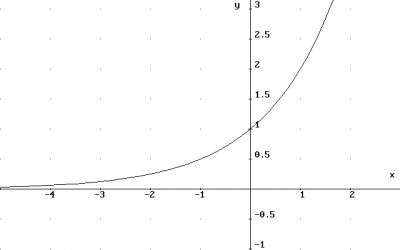
Función exponencial y ecuaciones logarítmicas

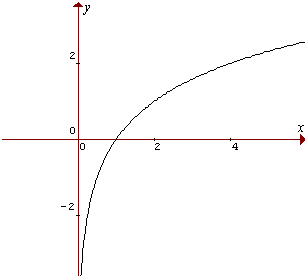
Propiedades de los logaritmo comunes: Para a > 1.

1) log_a 1 = 0

2) log_a a = 1

3) log_a (u v) = log_a u + log_a v

4) log_a (uⁿ) = n log_a u

5) log_a M = log_a N,  entonces M = N

 

Ejemplos para discusión:

1) Halla el valor de x si log₂ x - log₂ (x - 8) = 3.

2) Resuelve para x la ecuación:  log₈ 3 + ½ log₈ 25 = log₈ x .

Ejercicio de práctica: Resuelve log₄ (x + 1) - log₄ (3x - 2) = 2.

 

Función exponencial natural:

La letra a que aparece en la función exponencial se llama la base. La base puede ser cualquier número real positivo (ver definición de función exponencial). Sin embargo, hay casos donde se usa como base un número irracional denotado por e = 2.71828...

La función exponencial f(x) = e^x se conoce como la función exponencial natural.  :f(x) = e^x

 Logaritmo natural:

También podemos formar logaritmos con base e. Estos se llaman logaritmos naturales. Se representan por el símbolo ln. De manera, que si y = e^x, entonces x = log_e y = ln.

El logaritmo natural tiene todas las propiedades para logaritmos con base general a. En particular:

1) ln (u v) = ln (u) + ln (v)

3) ln uⁿ = n ln u

4) ln e = 1

5) ln 1 = 0

Ejercicios:

Escribe cada ecuación exponencial a la forma logarítmica y viceversa:

1) 2³ = 8

2) log₁₀ 0.01 = -2

3) ln 2 = 0.6931...

4) ln 0.5 = -0.6931...

Halla el valor de x:

7) log₁₀ 1000 = x

8) log₃ x = -110) log_x 27 = 3

9) log₃ x + log₃ (x - 2) = 1

10) x - 3 = log₂ 32

11) x² - x = log₅ 25

Dibuja la gráfica de :

12) f(x) = 3^x

13) y = 3^-x

Funciones exponenciales

  Repaso de funciones exponenciales

Las funciones lineales, cuadráticas, polinómicas y racionales se conocen como funciones algebraicas. Las funciones algebraicas son funciones que se pueden expresar en términos de operaciones algebraicas. Si una función no es algebraica se llama una función transcendental. Las funciones exponenciales, logarítmicas y trigonométricas son funciones transcendentales.

Definición: Una función exponencial es una función de la forma y = a^x, donde a>0 y a es diferente de uno.

F(x) = 2x	F(x) = (½)x = (2 -1)x = 2 -x

 Nota: Cuando (la base) a > 1 entonces la función exponencial es una función creciente, como lo es f(x) = 2^x. Mientras que cuando a < 1, la función exponencial es una función decreciente, como lo es f(x) = 2^-x.

Algunas características de las funciones exponenciales crecientes:

1) El dominio es el conjunto de los números reales.

2) El recorrido es el conjunto de los números reales positivos.

3) El valor de y se acerca a cero pero nunca será cero, cuando x toma valores negativos.

4) Todas las funciones intersecan al eje y en el punto (0,1).

5) Son funciones continuas.

Algunas características de las funciones exponenciales decrecientes:

1) El dominio es el conjunto de los números reales.

2) El recorrido es el conjunto de los números reales positivos.

3) El valor de y se acerca a cero pero nunca será cero, cuando x toma valores positivos.

4) Todas las funciones intersecan al eje y en el punto (0,1).

http://bc.inter.edu/facultad/ntoro/repasofunexpyloga.htm

Solución de ecuaciones cuadráticas

 Solución de la ecuación de segundo grado por medio de la factorizacion

 El método para solucionar ecuaciones de segundo grado por medio de la factorizacion es un poco complicado pero con algo de práctica se puede obtener cierta habilidad, este método se basa en que el producto de dos o más factores es cero, si cualquiera de los factores es cero.

De este modo la ecuación (X-4)(X-3) = 0 se satisface ya sea para X = 4 o para X= 3

Nota: Una buena habilidad adquirida en este método nos pueda dar buenos frutos en la solución de no solo ecuaciones  de segundo grado si no incluso de grado superior.

Los pasos a seguir son los siguientes:

Coloca todos los miembros del lado izquierdo de la ecuación e iguálalos a cero Factoriza el miembro de la izquierda en factores de primer grado. Cada factor así formado de primer grado se iguala a cero y se obtienen así las raíces.

Nota: Si no se cumple el primer paso entonces la ecuación no es factorizable.

Ahora bien te has de preguntar querido lector como se hace en la practica, pues aquí esta la solución con el siguiente ejemplo

X^2 = 2X + 3

X^2  - 2X - 3 = 0                       (Paso 1)

Para el caso dos el secreto esta en encontrar dos números que sumados nos den -2 y al multiplicarlos nos den como resultado - 3.

Esos números son -3 y 1 a continuación dichos números los sustituimos por -2 y la ecuación nos da como resultado:

X^2 - 3X + X -3 = 0

X(X - 3) + (X -3) = 0

(X + 1)(X - 3)=0                     (Paso 2)

Solución a la ecuación

X = -1

X = 3                                       (Paso 3)

No obstante, no siempre es fácil encontrar ambos números sobre todo si son cantidades grandes, ahora bien, un problema muy común es que en el primer término de la ecuación el coeficiente sea mayor a uno (A > 1) y es aquí donde tenemos una solución muy interesante para poder factorizar los términos.

Resulta que debemos multiplicar el coeficiente de X2 por el tercer término ( C ), lo que nos dará como resultado un número más grande.

Una vez que hemos hecho el paso anterior la tarea se centra en encontrar dos números que sumados nos el segundo termino y multiplicados nos den el numero grande encontrado.

Es así como funciona:

2X^2 - X -6 = 0

(2)(-6) = -12                            (Obtenemos el gran numero)

Los dos números son 3 y -4 los cuales sumados nos dan  - 1 y multiplicados nos dan -12 que es el gran numero obtenido.

2X^2 - 4X + 3X -6 = 0              (Sustitución de los dos números)

2X(X - 2) + 3(X - 2)               (Factorizacion por factor común)

(X - 2)(2X + 3) = 0                 (Ecuaciones de primer grado)

X = 2                                       (Resolución de las ecuaciones de primer grado)

X = -3/2

http://www.mailxmail.com/curso-diferentes-soluciones-resolver-ecuaciones-segundo-grado/solucion-ecuacion-segundo-grado-medio-factorizacion

 

 

Ecuaciones Lineales

Courtesy TerritorioScuola

Resolver una ecuación es encontrar todas su soluciones o llegar a la conclusión de que no tiene ninguna.

Ejemplo 1. a) x²-1=0 tiene dos soluciones, x =1 y x =-1

b) x² + 1=0 es una ecuación sin soluciones en R.

 c) 2x +3y = 0 tiene infinitas soluciones, (0,0), (-3,2), (3, -2)....

Ecuaciones equivalentes

Dos ecuaciones son equivalentes cuando admiten la mismas soluciones. Se cumple:

v     Si se suma o resta un mismo número a los dos miembros de una ecuación, se obtiene una ecuación equivalente a la primera.

v     Si se multiplican o dividen los dos miembros de una ecuación por un mismo número distinto de cero se obtiene una ecuación equivalente a la primera.

Trasposición de términos. Aplicando las reglas anteriores deducimos dos reglas prácticas:

Ø      Si un número aparece en un miembro sumando, se le puede pasar al otro miembro restando. Si esta restando pasará sumando.

Ø      De igual manera si está multiplicando pasa dividiendo y al revés.

Esto se llama trasponer términos.

Ejemplo 2:  La ecuación   5x - 1 = 2x -3    se puede escribir 3x + 2 = 0, trasponiendo términos.

Nota : El segundo miembro de la ecuación se puede considerar siempre que es 0.

Ecuaciones de primer grado

La forma general de esta ecuación es a x +b =0  con a0

Trasponiendo y dividiendo por a se llega  a  x = -b/a.

Solución que siempre existe y es única.

Ejemplo 3.  a) 3x +2 =0 Þ x = -2/3

b)  7x + 2 = 2x -3 , si  trasponemos términos, nos queda     7x –2x = -2 –3

Luego  5x = -5        de donde x = -1

Grafica de ecuaciones lineales

Gráfica de una ecuación lineal

Trazar la gráfica de 2x-5y=8

Solución                

Esta ecuación tiene la forma general de la ecuación de la recta (por lo tanto es una recta), de modo que basta determinar dos puntos en dicha representación. Se localizan las intersecciones con los ejes x y y, sustituyendo, respectivamente, y = 0 y x = 0 en 2x-5y = 8.

intersección con el eje x: Si y = 0 entonces
2x = 8, o sea, x = 4.

intersección con el eje y: Si x = 0 entonces
5y = 8, o sea, y = 8/5

Se localizan los puntos de coordenadas (4,0) y (0,8/5), y al trazar una recta que pase por ellos

Bienvenido

Ya tienes weblog.

Para empezar a publicar artículos y administrar tu nueva bitácora:

1. busca el enlace Administrar en esta misma página.
   
2. Deberás introducir tu clave para poder acceder.

Una vez dentro podrás:

• editar los artículos y comentarios (menú Artículos);
  
• publicar un nuevo texto (Escribir nuevo);
  
• modificar la apariencia y configurar tu bitácora (Opciones);
  
• volver a esta página y ver el blog tal y como lo verían tus visitantes (Salir al blog).

Puedes eliminar este artículo (en Artículos > eliminar). ¡Que lo disfrutes!